The Gradient Descent Algorithm
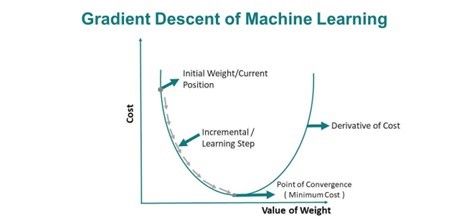
Descent a gradient is frequently applied in machine learning algorithms where the model parameters, for instance, weights, are adjusted for the model to improve its predictive power. The aim is to achieve the most negligible value of a cost function, which indicates the inaccuracy of a model’s prediction compared to the actual outcome. The cost function measures how well the model performs, and the goal is to minimize this function. The design utilizes minor alterations made to the parameters undertaken successively. Every step computes the gradient that depicts the most uphill cost surface direction. However, as the objective is to minimize cost, the approach advances against the gradient, moving “downhill” to lower cost function values. This is done repetitively until the cost function cannot be reduced anymore, and this infers the best values of the parameters for the model. The pace of this transition is governed by a constant learning rate that indicates how big each step should be. A very high learning rate may cause the algorithm to overlook the optimal values, while a shallow learning rate will make the minimum from the algorithm be achieved after a long time. Other versions of Gradient Descent, Stochastic, and Mini-Batch, for instance, perform the updates to the parameters in a slightly different way to speed up or enhance the process.
Variants of Gradient Descent
Batch Gradient Descent
Batch Gradient Descent is an essential method for training models to minimize errors by finding suitable parameter values in machine learning. This method uses the entire dataset to determine how the model's parameters will change, using every data point in each step before updating. Unlike other methods that make more frequent updates (such as after looking at one or a small group of data points), Batch Gradient Descent waits until it has checked the whole dataset. This approach ensures that each adjustment is more precise and stable, making it a reliable way to reach the best settings for the model. However, because it uses all the data every time, it can be slower and requires more memory, especially for large datasets.
Advantages:
Advantages:
- Convergence to Global Minimum: When the cost function has an excellent, bowl-like shape (convex), Batch Gradient Descent can find the lowest point, the global minimum. This means it finds the best possible settings for the model's parameters.
- Smooth Learning Process: Batch Gradient Descent calculates the gradient using the entire dataset, resulting in soft and consistent parameter updates. This stability makes the learning process more reliable and less noisy.
Disadvantages:
- High Memory and Computational Cost: Batch Gradient Descent processes the entire dataset in every step, demanding a lot of memory and computing power. This makes it challenging to use for massive datasets because as the data grows, it needs more memory than a typical computer can handle.
- Slow Convergence: Batch Gradient Descent uses the entire dataset for each update, making each step time-consuming, especially with large datasets. This slows the learning process and the search for the best model settings.
Use:
Batch Gradient Descent works best for small to medium-sized datasets where using the entire dataset for calculations is manageable. It’s a good choice when you need precise results and can afford to take more time, like when training models on data that easily fits into your computer’s memory. Since it uses all the data, its calculations are accurate and don’t have the random fluctuations seen in other methods. Nonetheless, batch-gradient descent may become prohibitively slow and memory-intensive when dealing with large datasets. In such situations, most of the time, Mini-Batch or Stochastic Gradient Descent are preferred because they allow more frequent updates to the model and reduce memory usage, thus enhancing the speed and efficiency of the learning process.
Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent (SGD) is a simplified and faster version of the gradient descent method used in machine learning. Unlike Batch Gradient Descent, which updates the model using the entire dataset, SGD makes updates using a single random data point or a small sample. This approach, which allows for quicker and more frequent updates, is beneficial when dealing with large datasets or real-time learning scenarios, offering practicality and convenience.
Advantages :
- Faster Updates: SGD updates the model much quicker because it only looks at one data point or a small sample. This makes it faster than Batch Gradient Descent, especially when working with large datasets.
- Escapes Local Minima: SGD's random updates help it avoid local minima and find better solutions, even with non-smooth cost functions.
- Lower Memory Usage: SGD processes one data point at a time, using less memory, making it great for limited computer power and massive datasets.
Disadvantages:
- Noisy Convergence Path: The changes may be random because SGD updates the model using only one data point at a time. This results in a loss function that jumps around instead of steadily decreasing, making the learning process less smooth and more unpredictable than Batch Gradient Descent.
- Risk of Overshooting: The updates are based on single data points, so the changes can vary, sometimes causing the model to overshoot the best solution, especially if the learning rate isn't set correctly.
Use:
SGD works well for enormous datasets because it doesn’t try to process all the data simultaneously, which would be too slow. It’s also great for online learning, where the model gets updated constantly with new data as it comes in. Because it can make quick updates and uses less memory, SGD is a popular choice in deep learning, especially for training complex models on big datasets.
Mini-Batch Gradient Descent
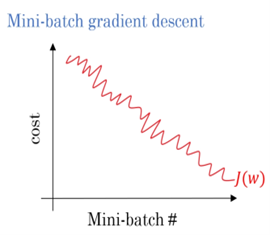
Mini-Batch Gradient Descent is a technique commonly employed to train machine learning models efficiently. It stands between the extremes of Batch Gradient Descent, where an entire dataset is considered simultaneously, and Stochastic Gradient Descent (SGD), which assumes one data point at a time. In Mini-Batch Gradient Descent, the model will make parameter updates using a small random data set known as a mini-batch. This enables the advantages of both methods to be utilized, making the training process more efficient. It introduces the control over the randomness present in the case of SGD without the slowness that comes with using the entire dataset, resulting in better performance when training models.
Advantages :
• Stable Convergence: Mini-Batch Gradient Descent smooths out updates compared to Stochastic Gradient Descent (SGD) by averaging changes from a mini-batch of data points. This leads to a steadier path toward finding the best solution.
• Efficient Hardware Usage: This method works well with modern computer hardware, especially GPUs, as it processes several mini-batches simultaneously, making training much faster.
• Faster Convergence: Mini-Batch Gradient Descent reaches the best solution quicker than Batch Gradient Descent by allowing more frequent updates while still benefiting from using multiple data points simultaneously.
Disadvantages:
• Tuning Required: Finding the right mini-batch size for Mini-Batch Gradient Descent is essential. If it's too small, it may not effectively reduce randomness; if it's too large, it may act more like Batch Gradient Descent.
• Higher Memory Usage: Mini-Batch Gradient Descent needs more memory than Stochastic Gradient Descent (SGD) because it processes multiple data points simultaneously. While it uses less memory than Batch Gradient Descent, it still requires enough memory to handle the mini-batch size for each update.
Use:
Mini-Batch Gradient Descent is often used in deep learning, especially for large datasets. It’s popular because it can process mini batches simultaneously using GPUs, which speeds up training.
Momentum-Based Gradient Descent
Momentum-based gradient descent is a method that enhances regular gradient descent by incorporating a memory feature. This memory assists the algorithm in retaining past updates, enabling it to gain momentum. Consequently, it facilitates a smoother learning process and expedites the model's attainment of the optimal solution.
Advantages :
Advantages :
• Accelerates Convergence: Momentum speeds up the learning process, especially in areas with slight gradients (or directions for updates). This helps move through flat parts of the loss landscape, where updates might otherwise slow down.
• Smooth's Noisy Updates: Momentum reduces random fluctuations in Stochastic Gradient Descent, leading to a more stable path to finding the best solution.
• Navigates Saddle Points: Momentum helps the algorithm bypass obstacles in the loss landscape, allowing it to move toward better solutions without getting stuck.
Disadvantages:
• Tuning Required: To get the best results from Momentum-Based Gradient Descent, you must carefully set both the learning rate and the momentum factor. Finding the correct values often takes testing and adjustments to see what works best.
Use:
Momentum-Based Gradient Descent is effective in deep learning models with complex loss landscapes. It can significantly accelerate the process of finding the best solution. This method is beneficial when regular Stochastic Gradient Descent (SGD) struggles to progress because its updates are too slow in challenging areas.


