Nov 26 / Swapnil Srivastava

Enhancing Model Performance: The Role of Regularization Techniques

Introduction to Regularization

Introduction to Regularization
Regularization is a helpful technique in machine learning that keeps models from becoming too complicated and overfitting the data. Overfitting happens when a model doesn't just learn the important patterns in the training data but also picks up on random noise or quirks. This makes the model perform really well on training data but poorly on new data, which is the opposite of what we want. Regularization adds a bit of a "penalty" to the model to prevent it from getting too complex, pushing it to be simpler and more focused on what's important. In the end, the goal is to create models that not only work well on the data they’ve seen but also perform reliably on new, unseen data.
Overfitting can lead to real problems because the model stops generalizing and becomes unreliable. For example, in healthcare or finance, where accuracy is critical, an overfitted model could make decisions based on random details in the data, which could have serious consequences. This is why regularization is so useful. It’s especially helpful when you have limited data, too many features, or a very complex model. It ensures the model isn’t just memorizing the data but learning the real patterns that will help it perform well in new situations.
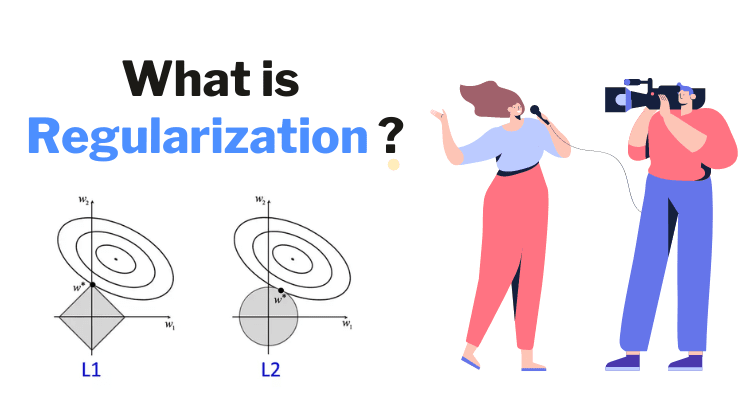
There are a few types of regularization that help achieve this. L1 regularization, often called Lasso, works by pushing some of the less important feature weights down to zero, essentially getting rid of them. This is like a built-in feature selection, helping simplify the model. L2 regularization, or Ridge, reduces the impact of each feature evenly, which is great for managing situations where multiple features are closely related. Finally, there’s Elastic Net, which combines L1 and L2, allowing for both feature selection and general weight reduction. This is especially useful when the dataset has many correlated features and you want the benefits of both approaches.

How Regularization Works

Regularization helps models stay simple and avoid overfitting by adding a penalty to the loss function. For example, in L1 regularization, this penalty is the sum of the absolute values of the model’s coefficients, while L2 regularization uses the sum of the squares of these coefficients. By introducing these penalties, the model is discouraged from becoming too complex and fitting the training data too closely. This leads to a simpler model that is more likely to perform well on new, unseen data. Regularization also helps balance bias and variance — even though it might slightly increase bias, it reduces variance significantly, improving the model’s overall performance.
The math behind regularization shows how this works. In L1 regularization, the penalty looks like \( \lambda \sum |w_i| \), and in L2, it’s \( \lambda \sum w_i^2 \), where \( \lambda \) is the regularization parameter that controls how much penalty is added. During gradient descent, the regularization term is included in the loss function, which affects how the model updates its parameters. This ensures that the model not only fits the data but also stays as simple as possible. The \( \lambda \) value plays a crucial role — a larger \( \lambda \) makes the model simpler, while a smaller \( \lambda \) allows it to fit the data more closely.
We can visualize the effects of regularization through graphs and case studies. For instance, a graph might show how a model performs on training data versus validation data, highlighting how regularization reduces overfitting. Real-world examples like predicting housing prices or classifying images demonstrate how regularization improves performance. Tools like TensorBoard or Matplotlib are commonly used to visualize these effects during model training, making it easier to track how regularization influences performance metrics and the learning process.

Common Regularization Techniques

L1 regularization, or Lasso, is really helpful when you suspect that many of the features in your dataset might not be that important. It works by reducing the impact of less relevant features, often pushing their coefficients all the way down to zero. This makes Lasso great for feature selection, especially in areas like genomics or text classification, where identifying the most important features is crucial. However, Lasso does have its limitations. When features are highly correlated, Lasso might arbitrarily pick one feature over another, which means it could miss some important information.
L2 regularization, or Ridge, takes a different approach. Instead of selecting a few key features, it shrinks all the coefficients, making it ideal for situations where you believe all the features are relevant but want to control their influence. Ridge is especially useful in cases of multicollinearity, where predictors are highly correlated. It helps stabilize the model and prevents overfitting by spreading out the impact across all features. This makes Ridge a go-to choice for problems like economic forecasting, where every feature likely plays a role, but their relationships can be complicated.
Dropout regularization is a technique mainly used in neural networks. It works by randomly "turning off" a fraction of the neurons during training, forcing the network to not rely too much on any single neuron. This helps the model become more resilient and generalize better to new data. Dropout is particularly useful in deep learning models, which tend to overfit due to their complexity. Unlike L1 and L2 regularization, which focus on adjusting the model's coefficients, dropout changes the actual structure of the neural network during training, making it a unique and powerful way to prevent overfitting.

Evaluating the Impact of Regularization

When evaluating how well a model performs, metrics like accuracy and precision are commonly used. Accuracy gives a general sense of how many predictions are correct, while precision specifically looks at how many of the model's positive predictions are actually right. In cases where the dataset is imbalanced, meaning there are more instances of one class than another, metrics like recall and the F1 score become more important. Recall helps us see how well the model captures all the relevant cases, and the F1 score balances both precision and recall for a more complete picture. To make sure the model is generalizing well and not just memorizing the training data, cross-validation is often used. This involves splitting the data multiple times into training and validation sets, providing a better test of the model’s performance.
Experimenting with different regularization techniques is essential to see what works best for a specific problem. By setting up controlled experiments, we can compare how various methods like L1 or L2 regularization impact the model. Analyzing these results helps us determine which technique improves the model’s performance. Case studies from real-world applications often show how regularization can make a significant difference, offering concrete examples of its value.
When it comes to using regularization effectively, the key is to choose the right technique based on the nature of the problem and the dataset. For instance, L1 regularization might be perfect if you want to eliminate irrelevant features, while L2 is better suited when all features matter. Tuning the regularization parameters, such as ( lambda ), is another crucial step in making sure the model is balanced between fitting the data well and remaining simple. It’s also important to keep an eye on how the model performs over time and adjust the regularization techniques as needed to keep the model performing at its best.

Future Trends in Regularization Techniques

Regularization methods are constantly improving, with new research bringing forth techniques that handle complex datasets better. These advancements often involve innovative algorithms that make models more adaptable and robust. Combining regularization with other methods, like ensemble learning, can further strengthen models by leveraging the benefits of multiple approaches. As automated machine learning becomes more common, effective regularization will be crucial for maintaining model reliability across various applications.
In cutting-edge fields, regularization is making a significant impact. In natural language processing (NLP), it helps improve how models work with text data by preventing them from overfitting and enhancing their ability to generalize. In computer vision, regularization is used to train models that perform well across different types of images, which is essential for tasks like recognizing objects. It's also starting to play a role in reinforcement learning, where it helps stabilize the learning process in complex environments.
However, there are challenges to consider. As models become more sophisticated, balancing regularization with interpretability can be tough. We need to ensure that regularization doesn't slow down training too much, as efficiency is key. Ethical concerns are also important—regularization techniques should be applied in ways that address biases in the data and ensure fair outcomes.
Future Trends in Regularization Techniques

Conclusion

In conclusion, regularization is a crucial tool in machine learning that helps prevent overfitting, ensuring that models perform well not just on training data but also on new, unseen data. By applying regularization techniques, practitioners can improve the generalization and reliability of their models, leading to better overall performance.

Understanding and utilizing these techniques is key to enhancing a model's effectiveness. As the field of machine learning continues to advance, it’s important to explore and experiment with various regularization methods. This ongoing exploration will be essential for developing robust models that can handle diverse and complex datasets effectively.

FAQs on Data Science Education in K-12:

  1. What is the main purpose of regularization in machine learning?
    The main purpose of regularization is to prevent overfitting by adding a penalty to the loss function, encouraging simpler models that generalize better.
  2. How do I choose between L1 and L2 regularization?
    Choosing between L1 and L2 regularization depends on your specific needs: use L1 for feature selection and L2 for handling multicollinearity.
  3. Can regularization be applied to all types of models?  
    Yes, regularization can be applied to various types of models, including linear regression, logistic regression, and neural networks.

  4. What are the signs that my model is overfitting?
    Signs of overfitting include high accuracy on training data but significantly lower accuracy on validation or test data.

  5. How can I effectively tune regularization parameters?
    Effective tuning of regularization parameters can be achieved through techniques like grid search or random search, often combined with cross-validation.

Created with